Physics-Informed Neural Network for 2D Heat Equation

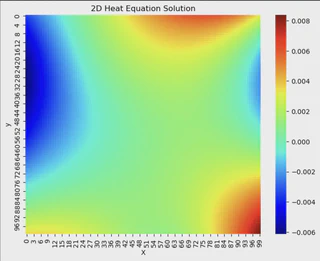
Built a physics-informed neural network in PyTorch that embeds the transient 2D heat equation PDE directly into the loss function, achieving high accuracy validated against finite-difference solvers.

Overview

This project demonstrates how neural networks can solve partial differential equations by incorporating physical laws directly into the training process. Unlike traditional data-driven approaches, PINNs respect governing equations as hard constraints.

Technical Approach

Architecture:

• Custom PyTorch neural network with physics-informed loss function
• Loss components: PDE residual + initial conditions + boundary conditions
• Network learns temperature distribution across space and time

PDE Integration:

• Embedded transient 2D heat equation: ∂T/∂t = α(∂²T/∂x² + ∂²T/∂y²)
• Automatic differentiation for computing spatial and temporal derivatives
• Boundary conditions enforced through penalty terms in loss function

Validation:

• Compared predictions against finite-difference numerical solver
• High accuracy achieved across spatial domain and time evolution
• Demonstrated advantage of mesh-free, continuous solutions

Key Technologies

• PyTorch for automatic differentiation and neural network implementation
• NumPy for finite-difference validation solver
• Matplotlib for visualization of temperature fields

Impact

Successfully showed that physical laws can guide neural network training, enabling solutions to PDEs without requiring large training datasets - the physics itself acts as supervision.